LC and some switches
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
Use T_1, T_3, and T_4 for T_1, T_3, and T_4, respectively as needed in this problems various parts. In addition, use pi for the constant \pi. You can use the standard trigonometric functions sin(arg), cos(arg), tan(arg), and inverse functions asin(arg), acos(arg), and atan(arg). You can use sqrt(arg) or do the root explicitly in python arg\*\*0.5.
The circuit shown below includes two switches: S1 and S2. Prior to t = 0, both switches are open, and the capacitor voltage v(t) and inductor current i(t) are both zero.
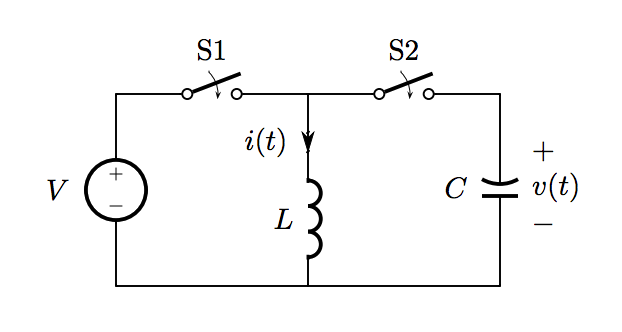
Part A
At t = 0, S1 closes, and it remains closed until t = T_1.
Determine the energy stored in the inductor w_L(t) at t = T_1. Enter T_1 as T_1.
Part B
At t = T_1, S1 opens as S2 simultaneously closes; the two switches change states so that they are not closed at the same time. The switches remain in their states until i(t) goes to zero, at which time S2 opens. Define the time at which i(t) goes to zero as t = T_2.
The energy stored in the inductor at t = T_1 is fully transferred to the capacitor at t = T_2. Use this fact to determine v(T_2). Note that this answer should match your answer to Part B of LC switches (I) when the latter is evaluated at t = T_2.
Part C
Both switches remain open until t = T_3. At t = T_3, S1 again closes, and it remains closed until t = T_4.
Determine the energy stored in the inductor w_L(t) at t = T_4.
Part D
Finally, at t = T_4, S1 opens as S2 again simultaneously closes. The switches remain in their states until i(t) again goes to zero, at which time S2 opens.
Use energy conservation to determine the energy stored in the capacitor at t = T_5, and then determine v(T_5). Note that this answer should match your answer to Part E of LC switches (I) when the latter is evaluated at t = T_5.
Part E
Now let the switches move repetitively through the three-step cycle described in LC switches (I): S1 initially closed with S2 open, next S1 open with S2 closed, finally both S1 and S2 open. Assume that in each cycle S1 remains closed for the duration T. Further, assume that S2 always opens when i(t) reaches zero. Assuming v(t) and i(t) are initially zero, determine v(t) at the end of the nth switching cycle in terms of n, C, L, T and V .