Frequency Response

The questions below are due on Friday April 28, 2023; 05:00:00 PM.

You are not logged in.
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.

In lab today we're going to get experience with analyzing our circuits using the impedance method and interpreting the results of that analysis. For this lab, we'll primarily be using our breadboards and few in-lab components. We will use today's lab to get some hands-on experience with the ideas from this week's lectures (impedance and frequency response).

In particular, we're hoping that you'll come away from this lab with some practical experience in a few new skills:

reading and understanding a Bode (gain vs. frequency) plot
understanding how the frequency-domain (Bode) plot contains information about time-domain plots
converting between dB and gain
using theory to design a filter to remove undesireable parts of a signal

Theory Warm-Up

We're going to start today by considering a familiar circuit:

Today we'll be doing a bunch of frequency analysis on circuits like these, but let's start by working out some theory (which should be familiar from the start of the week 10 pset). Answer the questions below to get started.

What is this circuit's time constant \tau, in terms of the circuit parameters?
Enter your answer as a Python expression below.

What is the ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)} in terms of the circuit parameters?
Enter your answer as a Python expression, using omega for \omega, j for j, R for R, and C for C.
HINT: Using the impedance method lets us treat this like a voltage divider!

What is the ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)} in terms of the time constant \tau?
Enter your answer as a Python expression, using omega for \omega, j for j, and tau for \tau.
HINT: Using the impedance method lets us treat this like a voltage divider!

As the frequency \omega approaches 0 (i.e., at low frequencies), what value does magnitude of the ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)} approach?

As the frequency \omega approaches \infty (i.e., at high frequencies), what value does magnitude of the ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)} approach?

Check Yourself 1:

What are the corresponding gains in dB at low and high frequencies?

What type of frequency response will this circuit exhibit?

At what value of \omega is the magnitude of the ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)} equal to 1\over \sqrt{2}?
Enter your answer in terms of tau (\tau).

What frequency f (measured in Hz) does that value of \omega correspond to?
Enter your answer as a symbolic expression in terms of tau (\tau)

At that frequency, what is the gain in dB?

At that frequency, what is the phase of ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)}, in degrees?

Getting Started

Before Building

Before building, let's reset the scope to all of its defaults by:

Pushing the "Default Setup" button in the upper left, and
Under the "Wave Gen" menu (accessible by pushing the button in the bottom right), click the "Settings" button (the bottom one on the screen), then click the "Default Wave Gen" button (the bottom one again) You should get a message on screen saying that things have been reset.

Really Getting Started

Get out your breadboard and get a few short wires. Grab a 110\Omega resistor and a 0.1{\rm \mu F} capacitor and build the circuit below:

The waveform generator from our scope will serve as V_{\rm sig} here, and we'll measure v_{in} using Channel 1 and v_{out} with Channel 2. Set up the wave generator with the following settings:

Sine Wave
1 kHz
1Vpp
0V offset

While watching the amplitudes of the two signals, gradually increase the frequency of the sine wave up to a few hundred kHz. Note you will need to periodically zoom in on the horizontal scale in order to keep being able to see the signal.

What do you notice as you increase the frequency?

What is the expected -3dB frequency (in Hz) of this RC circuit as predicted by theory?

Now, set the frequency to be this -3dB point you found earlier, and zoom things so you can clearly see channel 1 and channel 2 compared against each other. Measure the ratio of the amplitudes and eyeball the phase difference and make sure that they match your expected results from theory land.

Save this!

Take a photo of this measurement (including both channel 1 and channel 2) that clearly shows the amplitude ratio and phase offset! You will need both the photo and the measurements/results during checkoffs or later analysis.

Check Yourself 2:

How do these results compare against your theory work above?

Frequency Response

We would like to be able to characterize circuits' behaviors at a wide variety of frequencies (not just one). Given what we currently know, that would require us taking a whole bunch of measurements, changing the frequency of the wave gen manually, reading off some values, and then plotting them out like a chump. Thankfully our freiendly neighborhood scopes give us a better way to characterize the behavior of the circuits, a "frequency response analysis".

An Example Frequency Response

The plots that come from the frequency response analysis (Bode plots) were discussed in lecture, and we'll use this lab as an opportunity to deepen our understanding of what these plots mean. Before you do a frequency sweep, let's give a preview of what you'll eventually get. Consider the example frequency response curve below (for a different circuit than the one above):

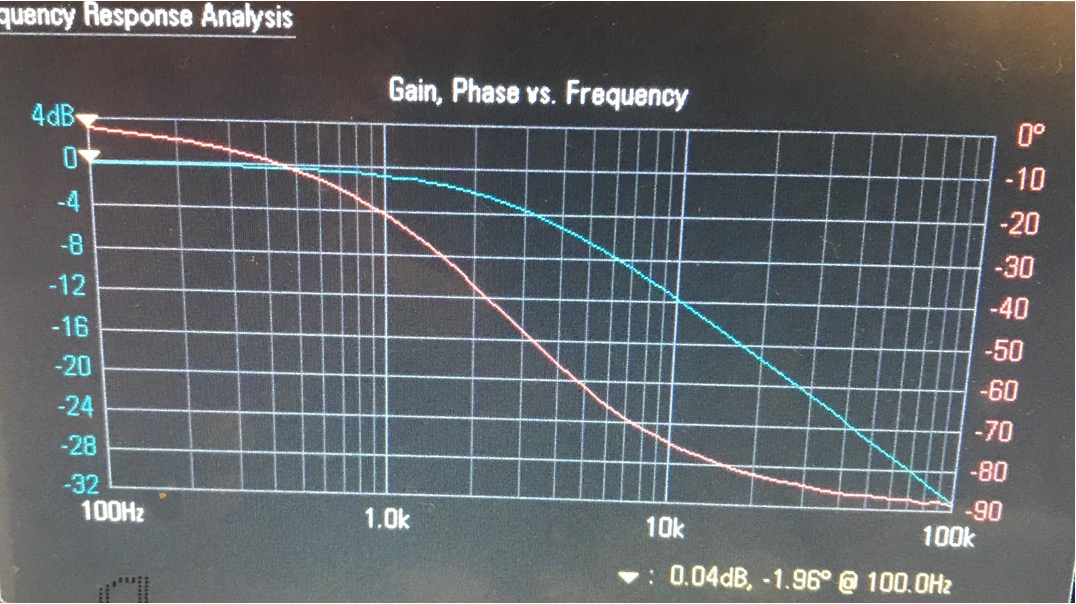
A Frequency Response Plot taken from a different circuit than the one you'll be analyzing. The blue plot is a plot of the gain (in dB) and the red is a plot of the phase in degrees. Note that the horizontal axis is on a log scale, but the labels are just the frequencies themselves.

Using the example plot above, answer the following questions:

At 100 Hz, what is the approximate gain (in dB) of this circuit?

For the gain in dB you found above, what voltage ratio does this gain correspond to (in other words, what is \frac{v_{out}}{v_{in}}) at that frequency?

At 70 kHz, what is the approximate gain (in dB) of this circuit?

For the approximate gain in dB you found in the previous question, what voltage ratio does this gain correspond to (in other words, what is \frac{v_{out}}{v_{in}} at that frequency?

At what approximate frequency (in Hz) is the magnitude of the output down by a factor of \frac{1}{\sqrt{2}} from its value at low (~100 Hz) frequencies?

When the magnitude of the gain is down by a factor of \frac{1}{\sqrt{2}} what does that correspond to in dB?

At the frequency where the magnitude of the gain is down by a factor of \frac{1}{\sqrt{2}} (previous question), what is the phase difference between the output and input (in radians)?

What is the approximate phase difference between the output and input as the frequency approaches 0 Hz? (answer in radians)?

What is the approximate phase difference between the output and input as the frequency approaches very high frequencies? (answer in radians)?

On Your Circuit

Now that we've gotten some practice with reading a Bode plot, let's go ahead and generate one. We'll use the same circuit from before:

With your circuit still the same and all your connections the same as before, go to Analyze >Features>Frequency Response Analysis. This should bring up a plot.

Then go to Setup and set:

Start Frequency at 10 Hz
Stop Frequency at 100 kHz
Amplitude at 1Vpp
Points at 100 (the number of frequencies to analyze)

Finally, press go. the screen will flash a bunch of sine waves as it sweeps 60 frequency points and analyzes the output over input ratio. When completed (after ~20 or 30 seconds), it'll give us a frequency response similar to what's shown below. The blue shows a plot of the magnitude (in dB) of \frac{v_{out}}{v_{in}} over frequency and the red is a plot of the phase (in degrees) of \frac{v_{out}}{v_{in}}. This should look very familiar based on the lectures this past week.

Using the "Entry" knob, identify what the -3dB point of your circuit is. Does it line up with your prediction from theory? Make sure it does! If not, ask for help!

Save this!

Take a photo of your circuit's frequency response! You will need it during checkoffs or later analysis.

The Ol' Switch-a-Roo-skie

Now let's make a little change and see what happens. In particular, let's swap the resistor and the capacitor like so:

After this change, what is the ratio \frac{v_\text{out}(j\omega)}{v_\text{in}(j\omega)}? Use "omega" for \omega and "j" for j and numbers for everything else.

What type of frequency response will this circuit exhibit?

Run an identical sweep on this circuit using the settings you previously used. Study the result and what do you see?

For high frequencies (>100 kHz) what approximate value does the gain approach (in dB)?

For low frequencies (<100 Hz) what approximate value does the phase approach (in radians)?

For high frequencies (>100 kHz) what approximate value does the phase approach (in radians)?

What is the -3dB frequency for this circuit? How does it compare against the version when the components were swapped?

Check Yourself 3:

Using circuit theory, what should the -3dB frequency be in terms of R and C (or in terms of \tau) for this circuit? How does that compare against what you saw in the low-pass version?

Save this!

Take a photo of your circuit's frequency response! You will need it during checkoffs or later analysis.

Checkoff 1:

Discuss what you've seen so far in lab. Be prepared to discuss the frequency responses of all your circuits including showing snapshots.

What do we expect to happen in a Low-Pass Filter?
What do we expect to happen in a High-Pass Filter?
What are common features shared by both types of filters?
How does a capacitor act at low/high frequencies?
- How do these ideas relate to the topologies we use for low-pass and high-pass filters with capacitors?
Explain your graphs of both sinusoids and frequency response analysis, and compare them against each other. What is the same and what is different?
Compare your graphs against the theory as well; how well does the theory predict the behavior we see?

Shuffling Off This Mortal Coil

Alright, we've tested a capacitive circuit. Now let's try an inductor. Consider the RL circuit below:

What is the ratio \frac{v_{out}(j\omega)}{v_{in}(j\omega)}? Use "omega" for \omega and "j" for j, L for L, and numbers for everything else.

Grab one of the inductors from up front (they're just a cute little pre-packaged coil of wire), as well as a 10{\rm k}\Omega resistor and build the circuit from above.

Let's run a frequency sweep on this thing. Use the following settings (BE CAREFUL TO GET THESE RIGHT):

Start Frequency at 100 Hz
Stop Frequency at 100 kHz
Amplitude at 200mVpp
Points at 60 (the number of frequencies to analyze)

Press Run Analysis and study your frequency response!

Using the "Entry" knob, determine the -3dB point and then back out what the inductance must be.

What is the inductance of this coil in Henries?

A Design Task

Knowledge of frequency response can be very powerful. Let's get some practice using filters, rather than just studying them by designing a filter that lets through only a signal that we care about and blocks out other stuff. In order to create this situation we're going to start with a 1Vpp Sine wave at a frequency of 800 Hz and then add stuff on top of it. Set up your oscilloscope so Channel 1 is measuring this signal. Verify that you have a a nice clean sinewave. Turn on BW Limit if you haven't already. The first thing we'll do is to add noise: Under the WaveGen Menu, go to Settings > Noise and crank it all the way to 100%. You should notice the signal has gotten fuzzier with high frequency noise. Although we're doing this synthetically here, it's normal for our real-world measurements to be naturally corrupted by noise, so this knowledge is useful for real stuff, too...

Now the second thing we'll do is add some more structure noise in the form of modulation. Go to Settings > Modulation and turn on the following settings:

Type: AM
Waveform: Sine
AM Freq: 20 kHz
AM Depth: 100%

Then turn on the modulation by making sure the little box under the Modulation option in the menu is colored in. What this will do is add additional disinct frequency components at several higher frequencies on top of our 800 Hz base signal. If you measure this waveform with Channel 1, you should expect to see the following signal shown below:

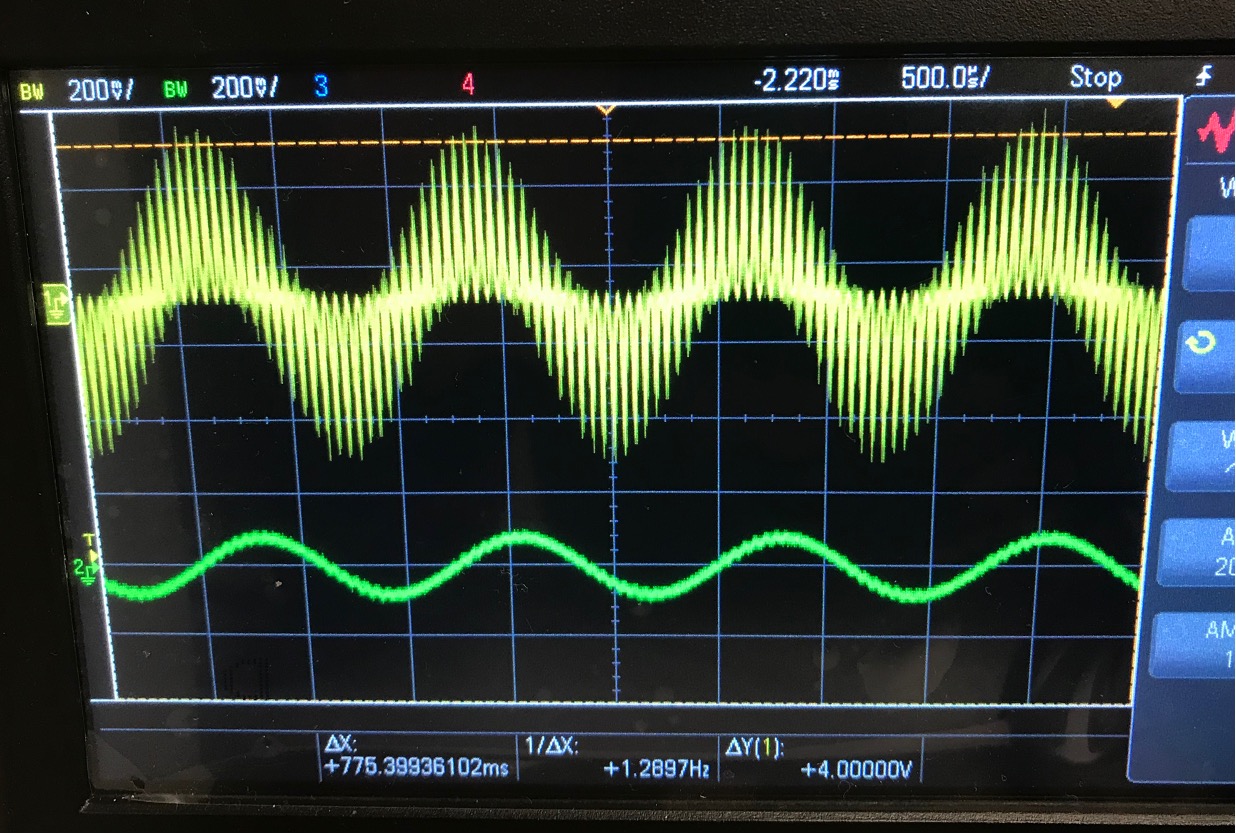
The expected input signal (on channel 1) and the approximate output signal we'd like to work obtain (on channel 2).

What we'd like you to do now is to tune your LR circuit to filter out the majority of the "undesired" frequency components of the merged V_{\rm sig} signal (noise and high frequency modulation artifacts), leaving largely just the 800 Hz signal intact as shown in the Figure above.

This is very similar to what one would need to do in a wireless communication device or other things. But anyways for now, using parts available in lab, design a low pass filter that:

Passes 800 Hz (gives at least a 200mV peak-to-peak signal from the 800Hz component)
Blocks most or a good chunk of the ~20 kHz signals as well as the high frequency noise.

There is no "right" answer for how to do this, but as a hint, try to place the -3dB point between the two frequencies of interest. If it's too high, your filter will let too much 20kHz through; and if it's too low, your filter will block too much 800 Hz signal.

As you're working through, feel free not only to look at the results in terms of the two sine waves, but also to run additional frequency response analyses and/or to go back to the theory.

When you have gotten your filter working, be ready to show it to a staff member for checkoff. Explain your design choices and show it in operation.

Checkoff 2:
Discuss your results in the second half of the lab.

How did you determine the inductance of the coils we have?
Show the results of your filtering and discuss your process.
- What cutoff frequency did you target?
- How did you adjust your circuit values to hit this cutoff frequency?

When you're done, bring your inductor and breadboard back. But it's fine to chuck your capacitors and resistors.

Please also clean up your lab space. Be a good citizen of the world and leave it cleaner than you found it. That means throwing out trash (including unused wires), hanging up the scope probes, resetting everything on the scope to default settings, using your turn signals when driving, etc.