Big KCL and Tellegen
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
1) Part 1: Wide-area KCL
A sub-network, which is a portion of a larger network, is shown below. Only the three branch currents i_A, i_B and i_C enter this sub-network. Show that KCL is satisfied across the sub-network. That is, show that i_A +i_B +i_C = 0. This must be true following charge conservation, and the fact that nodes and circuit elements in 6.200 do not store net charge.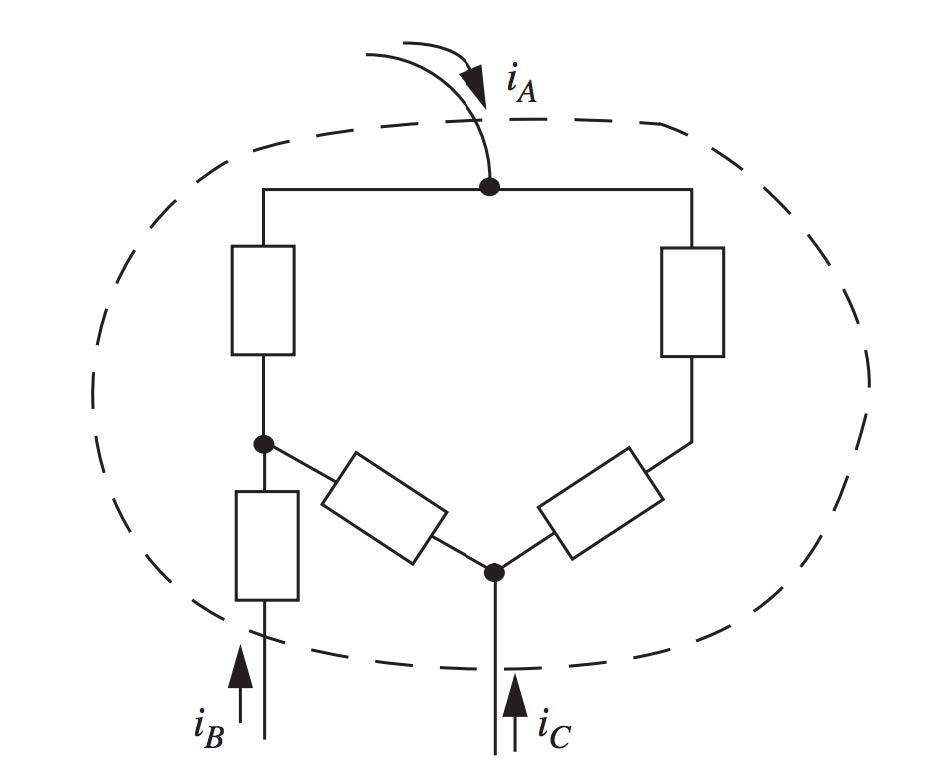
2) Part 2: Power & Tellegen
This problem concerns the networks shown below. The devices in the network are drawn as non- specific boxes, indicating that they might each be a source or a resistor.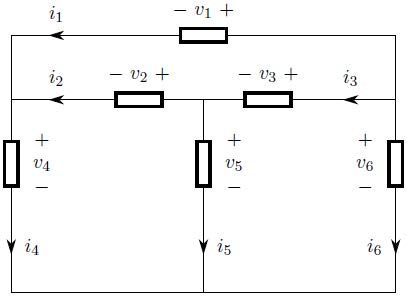
With the restriction that they must satisfy KVL, assign otherwise arbitrary values to the device
voltages v_1 through v_6. You choose the values; not all zero, please. Similarly, with the restriction
that they must satisfy KCL, assign otherwise arbitrary values to the device currents i_1 through i_6.
Again you choose the values; again not all zero, please. Next, compute the power into each device.
Make a table showing the voltage, current, and power for each device. Finally, sum the powers into
the six devices and note that their sum is zero.
The remarkable result found demonstrated above, which follows from Tellegen's theorem, illustrates
that power is always conserved in an electrical network independent of the elements in the network.
(Note that your assignment of the voltages and currents was carried out independently, and thus
not predicated on the behavior of any of the network elements.) Further, the same is true for any
physical system that can be modeled with electrical networks. For more on Tellegen's Theorem,
see Introductory Network Theory by Bose and Stevens, Harper & Row, 1965, for example, or the
Wikipedia page for Tellegen's Theorem.